Exercises from "Fundamentals of Astrodynamics" Part 2

24 Aug 2019

Continuing with the first problem set in “Fundamentals of Astrodynamics” by Bate, Mueller, and White, we arrive at what seems like simple problem. Given the velocity and position of a satellite, find its eccentricity. However, as simple as it seems, you’ll see it takes quite a bit of derivation to arrive at the answer.

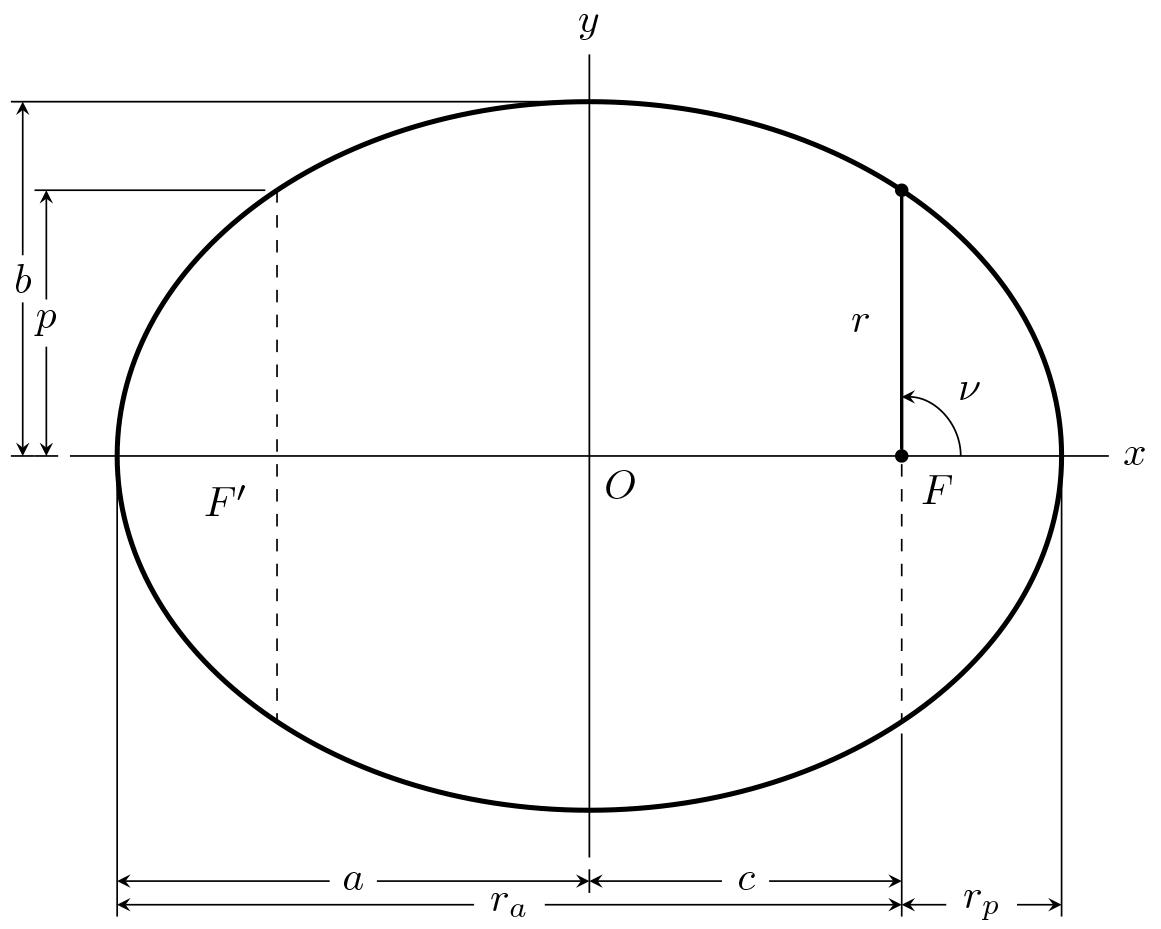
Exercise 1.2 For a certain satellite the observed velocity and radius at $\nu = 90^\circ$ is observed to be 45,000 ft/s and 4000 NM, respectively. Find the eccentricity of the orbit.

Solution:

To begin, by inspection of Figure 1.5-1 in the book or the figure above, $r = p$ when $\nu = 90^\circ$. We can also show this mathematically using the polar equation of a conic section:

$$\begin{align*} r &= \frac{p}{1 + e\cos{\nu}} \\ &= \frac{p}{1 + e\cos{90^\circ}} \\ &= \frac{p}{1 + 0} \\ &= p, \end{align*}$$

where $r$ is the radius, $p$ is the semi-latus rectum, and $e$ is the eccentricity.

Using equation 1.5 between the semi-major axis, $a$, and the semi-latus rectum, $p$, we can solve for eccentricity:

$$\begin{align*} p &= a(1 - e^2) \\ \therefore e &= \sqrt{1 - \frac{p}{a}} \\ \because p &= r \\ e &= \sqrt{1 - \frac{r}{a}}. \end{align*}$$

Now we need to find, $a$. This can be done using the relationship between $a$ and the specific mechanical energy, $\mathcal{E}$:

$$\begin{align*} \mathcal{E} &= - \frac{\mu}{2a} \\ \therefore a &= - \frac{\mu}{2\mathcal{E}}, \\ \end{align*}$$

where $\mu$ is the gravitational parameter, 1.40765x10¹⁶ ft³s^-2 for Earth.

Substituting this into our equation for $e$ yields:

$$\begin{align*} e &= \sqrt{1 - \frac{r}{- \frac{\mu}{2\mathcal{E}}}} \\ &= \sqrt{1 + \frac{2r\mathcal{E}}{\mu}}. \end{align*}$$

Recall that the equation for specific mechanical energy is:

$$\mathcal{E} = \frac{v^2}{2} - \frac{\mu}{r}.$$

Substituting this into our equation for $e$ above, with a little rearranging, gives us eccentricity in terms of our knowns:

$$\begin{align*} e &= \sqrt{1 + \frac{2r}{\mu} \left ( \frac{v^2}{2} - \frac{\mu}{r} \right )}\\ &= \sqrt{1 + \frac{v^2r}{\mu} - 2 } \\ &= \sqrt{\frac{v^2r}{\mu} - 1 }. \end{align*}$$

Now the calculation for eccentricity can be done being mindful of units (1 NM = 6076.12 ft):

$$\begin{align*} \therefore e &= \sqrt{\frac{(45000)^2(4000*6076.12)}{1.40765*10^{16}}-1} \\ &= 1.581, \end{align*}$$

which means the orbit is hyperbolic.

eccentricity